

In Maths, the composition of a function is an operation where two functions say f and g generate a new function say h in such a way that h(x) = g(f(x)). It means here function g is applied to the function of x. So, basically, a function is applied to the result of another function.
Let’s have a look at the definition of a composite function .
Let f : A → B and g : B → C be two functions. Then the composition of f and g, denoted by g ∘ f, is defined as the function g ∘ f : A → C given by g ∘ f (x) = g(f (x)), ∀ x ∈ A.
The below figure shows the representation of composite functions .
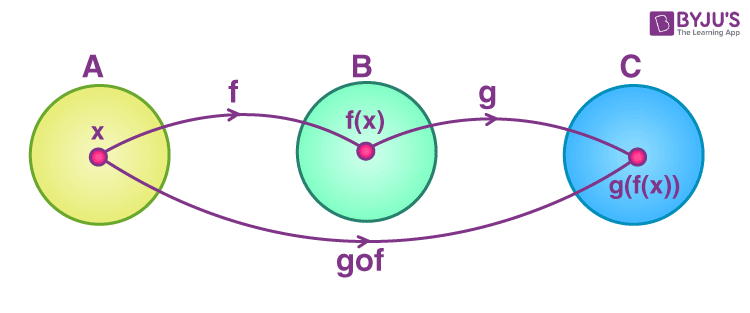
The order of function is an important thing while dealing with the composition of functions since (f ∘ g) (x) is not equal to (g ∘ f) (x).
The relation and function is an important concept of Class 11 and 12. See below the function composition symbol and domain with example.
Symbol: It is also denoted as (g∘f)(x), where ∘ is a small circle symbol. We cannot replace ∘ with a dot (.), because it will show as the product of two functions, such as (g.f)(x).
Domain: f(g(x)) is read as f of g of x. In the composition of (f o g) (x) the domain of function f becomes g(x). The domain is a set of all values which go into the function.
Example: If f(x) = 3x+1 and g(x) = x 2 , then f of g of x, f(g(x)) = f(x 2 ) = 3x 2 +1.
If we reverse the function operation, such as f of f of x, g(f(x)) = g(3x+1) = (3x+1) 2
Also, read:
Associative Property: As per the associative property of function composition, if there are three functions f, g and h, then they are said to be associative if and only if;
f ∘ (g ∘ h) = (f ∘ g) ∘ h
Commutative Property: Two functions f and g are said to be commute with each other, if and only if;
g ∘ f = f ∘ g
Few more properties are:
In maths, solving a composite function signifies getting the composition of two functions. A small circle (∘) is used to denote the composition of a function.
Go through the below-given steps to understand how to solve the given composite function.
Step 1: First write the given composition in a different way.
Consider f(x) = x 2 and g(x) = 3x
(f ∘ g) (x) can be written as f[g(x)].
Step 2: Substitute the variable x that is there in the outside function with the inside function by taking the individual functions as a reference.
Step 3: Finally, simplify the obtained function.
(f ∘ g)(x) = f(3x) = (3x) 2
It is possible to compose a function with itself. Suppose f is a function, then the composition of function f with itself will be
Let us understand this with an example:
Example: If f(x) = 3x 2 , then find (f∘f)(x).
Solution: Given: f(x) = 3x 2
Q.1: If f (x) = 2x and g(x) = x+1, then find (f∘g)(x) if x = 1.
Solution: Given, f(x) = 2x
Therefore, the composition of f from g will be;
Now putting the value of x = 1
f(g(1)) = 2(1+1) = 2 (2) = 4
Q.2: If f(x) = 2x +1 and g(x) = -x 2 , then find (g∘f)(x) for x = 2.
g(f(x)) = g(2x+1) = -(2x+1) 2
Now put x =2 to get;
Q.3: If there are three functions, such as f(x) = x, g(x) = 2x and h(x) = 3x. Then find the composition of these functions such as [f ∘ (g ∘ h)] (x) for x = -1.
To find: [f ∘ (g ∘ h)] (x)
[f ∘ (g ∘ h)] (x) = f ∘ (g(h(x)))
[f ∘ (g ∘ h)] (-1) = 6(-1) = -6